Материал подготовлен Юлией Кельман
Объяснение интерференции световых волн можно начать с ответа на вопрос: «Что происходит в определенной точке в пространстве, когда две световые волны проходят эту точку одновременно?» Чтобы ответить на этот вопрос мы прибегаем к принципу суперпозиции, который утверждает, что:
Когда две или более волны одновременно распространяются в определенном пространстве, каждая волна распространяется независимо, как будто другие не существуют. Получающееся "смещение" волны в любой точке в любое время равняется векторной сумме "смещений" отдельных волн.
Этот принцип остается справедливым для волн на воде, механических волн на бечевках и пружинах и для звуковых волн в газах, жидкостях и твердых веществах.
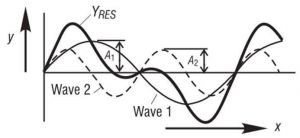 Наиболее важным для настоящей работы является то, что он остается справедливым для всех электромагнитных волн в свободном пространстве. Итак, если две волны проходят через общую точку P, в которой волна 1 вызывает смещение Y1, а волна 2 - смещение Y2, то принцип суперпозиции утверждает, что получающееся смещение YRES получается из векторной суммы этих двух смещений. Если оба смещения имеют одно и то же направление - что будет происходить в большинстве случаев в этом модуле – мы можем сложить их алгебраически.
Наиболее важным для настоящей работы является то, что он остается справедливым для всех электромагнитных волн в свободном пространстве. Итак, если две волны проходят через общую точку P, в которой волна 1 вызывает смещение Y1, а волна 2 - смещение Y2, то принцип суперпозиции утверждает, что получающееся смещение YRES получается из векторной суммы этих двух смещений. Если оба смещения имеют одно и то же направление - что будет происходить в большинстве случаев в этом модуле – мы можем сложить их алгебраически.
На рисунке показан результат сложения двух волн 1 и 2, распространяющихся в направлении Х вправо. Волна 2 изображена с амплитудой ¾ и ½ длины волны 1. Итоговая волна показана жирной линией Y RES.
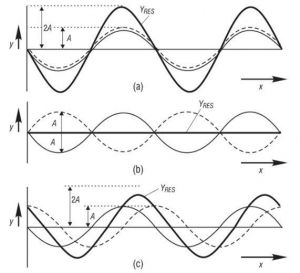 На Рис. 2 показана интерференция двух синусоидальных волн одинаковой амплитуды и частоты, распространяющихся в одном направлении. Эти две волны представлены светлой жирной линией и светлой пунктирной линией, а результат – темной жирной кривой. На графике 2а две волны точно совпадают в фазах, точки максимума и минимума совпадают полностью. Если применить принцип суперпозиции к этим двум волнам, то, как видно, по сравнению с ними, итоговая волна имеет такую же амплитуду и частоту, но вдвое большую амплитуду 2a. Это является примером конструктивной интерференции.
На Рис. 2 показана интерференция двух синусоидальных волн одинаковой амплитуды и частоты, распространяющихся в одном направлении. Эти две волны представлены светлой жирной линией и светлой пунктирной линией, а результат – темной жирной кривой. На графике 2а две волны точно совпадают в фазах, точки максимума и минимума совпадают полностью. Если применить принцип суперпозиции к этим двум волнам, то, как видно, по сравнению с ними, итоговая волна имеет такую же амплитуду и частоту, но вдвое большую амплитуду 2a. Это является примером конструктивной интерференции.
На графике 2b две кривые абсолютно не синхронны, при этом точка максимума одной совпадает с точкой минимума другой, и так далее. Так как одна волна эффективно гасит амплитуду другой для каждой взятой точки, итоговая волна имеет нулевое смещение по всей длине, на что указывает жирная черная линия. Это является примером деструктивной интерференции.
На графике 2с, представленные две волны не являются ни полностью синхронными, ни полностью асинхронными. В данном случае итоговая волна имеет амплитуду между А и А2, как и показано на графике.